Is Tom DeMark Sequential Indicator Profitable in Eur/Usd Swing Trading ?

I used the same programming code of Hang Seng Index to backtest the performance of Tom DeMark Sequential Indicator applying on Daily Eur/Usd data. I found similar performance of the indicator used in Hang Seng Index trading. The following two charts show the result of Non-Perfect and Perfect setup / countdown. The targets include 0.236, 0.386, 0.5, 0.618, 0.764, 1, 1.272 and 1.618.
It can be seen that the highest return is obtained at 1.272 target. Besides, it is obvious that the smaller the target ratio is, the smaller the profit is. The Perfect setup and countdown may have better result than the non-perfect setup and countdown.

Looking at the highest annual gain of 1.272 target from 1996 to March 2013, it is only about 300 pips, it is not much compared with the drawdown.

Although it seems that Tom DeMark Sequential Indicator does not have good return, it is possible to have bigger return if the indicator is modified. I'll post another blog article to describe a modified use of the indicator.

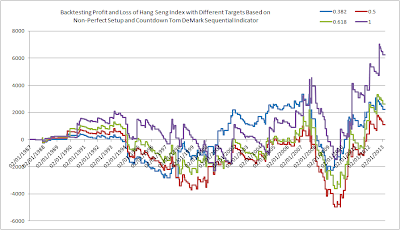
Is Tom DeMark Sequential Indicator(TM) Profitable in Hang Seng Index ?

Tom DeMark Sequential is a famous indicator in professional financial package like Bloomberg and Reuters. Kurt Magnus, head of Forex sales at Westpac bank in London said that it was 70% reliable, and even closer to 90% in Forex.

It arouses my interest to see if it can be used in Hang Seng Index. I developed my indicator based on Tom DeMark's published theory and back test it for 20 years of Hang Seng Index Daily data captured from Yahoo. My stop loss is a little different from Tom's theory. Instead of waiting the daily price closing to confirm stop loss, I trigger the stop loss immediately when it reaches. My target is based on the lowest price value from the beginning of the setup to the end of the countdown for long trade, and the highest price value for short trade.

Then I look for 0.382, 0.5, 0.618 and 1 times of the target value from the order placement price. The following two charts respectively plot the profit and loss over the test period for Non-Perfect and Perfect Setup and Countdown similar to Tom's theory. It can be seen that a larger target has higher profit no matter whether it is perfect or not. Besides, the perfect setup and countdown is not guaranteed to more profit over the period. However, the profit gained over the years is not impressing compared to the gain of the Hang Seng Index itself in the same period.

More results will be posted later.

Is Flag or High Tight Flag pattern profitable in Forex market ?

I test the performance of Flag / High Tight Flag patterns for the major Forex currency data from 4/1/2011 to 26/6/2012. It is found that these patterns are quite profitable as similar to other people claimed before about their profitability in the stock market.

The currency pairs I test include Eur/Usd, Usd/Jpy, Gbp/Usd and Usd/Chf. The equity charts assume that each time a 2 lots mini contract (US$10,000) is placed, the stop loss is set to 10 pips below the channel of the flag and the breakout price is assumed at 20 pips above the flag channel for a bull flag. Similar setting of stop loss and breakout price is used for the bear flag. The contracts are closed if the price reaches 0.764 extension level from the breakout. There will be a loss if the price hits the stop loss first. The chart shown below has included the bid/ask spread cost of the currency pair but does not include the roll over interest of the pair.

The Flag / High Tight Flag pattern performs well in the first 11 months of 2011 but has a loss of about US$1600 from Dec 2011 to June 2012. The 6 months bad performance of the Flag / High Tight Flag pattern is not what I like although it is generally good in performance compared to other chart patterns.

How many days to wait for a rebound after a fall in S&P 500 ?

I used different window sizes, from 10 to 99 days, to find the maximum in window.

For example, if a window of 20 days is used, the algorithm looks for the maximum in the past 20 days. After the maximum is found, there should be some local minima and local maxima occurred in these 20 days. The local maxima must be smaller than the maximum in the whole 20 days period. These maxima are actually the several rebounds of the fall from the maximum in the past 20 days.

As I tune the window size from 10 to 99 days, I can calculate the percentage of a rebound occurred in any one day of the whole window period. A valid rebound is the lowest price tomorrow not less than today's lowest price after the rebound. Obviously, the percentage should gradually drop as the window increases because there are more points in the window so the maxima should spread out. Nonetheless, there is still a high percentage of a rebound occurred in the next 7 days after a maximum is found for the window.

For example, the following table shows the cumulative frequency with a 20 days window. The maximum number of days may be 1 day more than the window size. It is because in the past 20 days, the trend is down and the maximum occurs 20 days ago, if tomorrow's price is higher than today's lowest price, it is counted as a rebound in the 21st day after the maximum. There is 11.65% chance of a rebound after a fall from a maximum found today. There is 81.6% of chance the rebound occurred in the next 7 days for a 20 days window. The percentage of a rebound in the next 7 days is more than 66% even for a 99 days window.

20 Days Window :

21 days	1348	Percentage	Cumulative Freq
0	157	11.65%	11.65%
1	341	25.30%	36.94%
2	217	16.10%	53.04%
3	127	9.42%	62.46%
4	89	6.60%	69.07%
5	65	4.82%	73.89%
6	45	3.34%	77.23%
7	59	4.38%	81.60%
8	32	2.37%	83.98%
9	28	2.08%	86.05%
10	30	2.23%	88.28%
11	21	1.56%	89.84%
12	18	1.34%	91.17%
13	14	1.04%	92.21%
14	22	1.63%	93.84%
15	19	1.41%	95.25%
16	12	0.89%	96.14%
17	15	1.11%	97.26%
18	13	0.96%	98.22%
19	16	1.19%	99.41%
20	7	0.52%	99.93%
21	1	0.07%	100.00%

The following tables list the cumulative frequency of a rebound in window of 10, 30, 40, 50, 90 and 99 days respectively.

10 Days Window :

11 days	1577	Percentage	Cumulative Freq
0	195	12.37%	12.37%
1	472	29.93%	42.30%
2	281	17.82%	60.11%
3	175	11.10%	71.21%
4	125	7.93%	79.14%
5	93	5.90%	85.03%
6	55	3.49%	88.52%
7	71	4.50%	93.02%
8	42	2.66%	95.69%
9	31	1.97%	97.65%
10	35	2.22%	99.87%
11	2	0.13%	100.00%

30 Days Window :

30 days	1216	Percentage	Cumulative Freq
0	136	11.18%	11.18%
1	286	23.52%	34.70%
2	167	13.73%	48.44%
3	110	9.05%	57.48%
4	72	5.92%	63.40%
5	57	4.69%	68.09%
6	34	2.80%	70.89%
7	54	4.44%	75.33%
8	31	2.55%	77.88%
9	20	1.64%	79.52%
10	28	2.30%	81.83%
11	16	1.32%	83.14%
12	19	1.56%	84.70%
13	15	1.23%	85.94%
14	20	1.64%	87.58%
15	19	1.56%	89.14%
16	13	1.07%	90.21%
17	16	1.32%	91.53%
18	13	1.07%	92.60%
19	13	1.07%	93.67%
20	7	0.58%	94.24%
21	9	0.74%	94.98%
22	14	1.15%	96.13%
23	6	0.49%	96.63%
24	7	0.58%	97.20%
25	4	0.33%	97.53%
26	3	0.25%	97.78%
27	9	0.74%	98.52%
28	2	0.16%	98.68%
29	9	0.74%	99.42%
30	7	0.58%	100.00%

40 Days Window :

40 days	1123	Percentage	Cumulative Freq
0	131	11.67%	11.67%
1	239	21.28%	32.95%
2	152	13.54%	46.48%
3	97	8.64%	55.12%
4	67	5.97%	61.09%
5	52	4.63%	65.72%
6	27	2.40%	68.12%
7	46	4.10%	72.22%
8	28	2.49%	74.71%
9	21	1.87%	76.58%
10	26	2.32%	78.90%
11	15	1.34%	80.23%
12	16	1.42%	81.66%
13	13	1.16%	82.81%
14	15	1.34%	84.15%
15	17	1.51%	85.66%
16	11	0.98%	86.64%
17	13	1.16%	87.80%
18	11	0.98%	88.78%
19	13	1.16%	89.94%
20	5	0.45%	90.38%
21	10	0.89%	91.27%
22	13	1.16%	92.43%
23	6	0.53%	92.97%
24	7	0.62%	93.59%
25	4	0.36%	93.94%
26	3	0.27%	94.21%
27	8	0.71%	94.92%
28	2	0.18%	95.10%
29	8	0.71%	95.81%
30	8	0.71%	96.53%
31	8	0.71%	97.24%
32	4	0.36%	97.60%
33	5	0.45%	98.04%
34	4	0.36%	98.40%
35	2	0.18%	98.58%
36	3	0.27%	98.84%
37	4	0.36%	99.20%
38	2	0.18%	99.38%
39	4	0.36%	99.73%
40	3	0.27%	100.00%

50 Days Window :

50 days	1042	Percentage	Cumulative Freq
0	117	11.23%	11.23%
1	230	22.07%	33.30%
2	129	12.38%	45.68%
3	90	8.64%	54.32%
4	57	5.47%	59.79%
5	42	4.03%	63.82%
6	23	2.21%	66.03%
7	42	4.03%	70.06%
8	21	2.02%	72.07%
9	19	1.82%	73.90%
10	24	2.30%	76.20%
11	14	1.34%	77.54%
12	16	1.54%	79.08%
13	11	1.06%	80.13%
14	14	1.34%	81.48%
15	18	1.73%	83.21%
16	9	0.86%	84.07%
17	14	1.34%	85.41%
18	9	0.86%	86.28%
19	12	1.15%	87.43%
20	7	0.67%	88.10%
21	8	0.77%	88.87%
22	11	1.06%	89.92%
23	7	0.67%	90.60%
24	8	0.77%	91.36%
25	4	0.38%	91.75%
26	4	0.38%	92.13%
27	6	0.58%	92.71%
28	1	0.10%	92.80%
29	7	0.67%	93.47%
30	6	0.58%	94.05%
31	9	0.86%	94.91%
32	3	0.29%	95.20%
33	6	0.58%	95.78%
34	3	0.29%	96.07%
35	1	0.10%	96.16%
36	2	0.19%	96.35%
37	4	0.38%	96.74%
38	2	0.19%	96.93%
39	4	0.38%	97.31%
40	3	0.29%	97.60%
41	2	0.19%	97.79%
42	0	0.00%	97.79%
43	6	0.58%	98.37%
44	0	0.00%	98.37%
45	4	0.38%	98.75%
46	0	0.00%	98.75%
47	3	0.29%	99.04%
48	3	0.29%	99.33%
49	3	0.29%	99.62%
50	4	0.38%	100.00%

90 Days Window :

87 days	889	Percentage	Cumulative Freq
0	95	10.69%	10.69%
1	188	21.15%	31.83%
2	105	11.81%	43.64%
3	77	8.66%	52.31%
4	48	5.40%	57.71%
5	31	3.49%	61.19%
6	18	2.02%	63.22%
7	34	3.82%	67.04%
8	18	2.02%	69.07%
9	17	1.91%	70.98%
10	20	2.25%	73.23%
11	11	1.24%	74.47%
12	15	1.69%	76.15%
13	10	1.12%	77.28%
14	14	1.57%	78.85%
15	15	1.69%	80.54%
16	8	0.90%	81.44%
17	10	1.12%	82.56%
18	12	1.35%	83.91%
19	10	1.12%	85.04%
20	6	0.67%	85.71%
21	6	0.67%	86.39%
22	7	0.79%	87.18%
23	6	0.67%	87.85%
24	8	0.90%	88.75%
25	1	0.11%	88.86%
26	4	0.45%	89.31%
27	4	0.45%	89.76%
28	1	0.11%	89.88%
29	6	0.67%	90.55%
30	5	0.56%	91.11%
31	8	0.90%	92.01%
32	1	0.11%	92.13%
33	5	0.56%	92.69%
34	1	0.11%	92.80%
35	1	0.11%	92.91%
36	6	0.67%	93.59%
37	2	0.22%	93.81%
38	3	0.34%	94.15%
39	4	0.45%	94.60%
40	3	0.34%	94.94%
41	1	0.11%	95.05%
42	1	0.11%	95.16%
43	4	0.45%	95.61%
44	0	0.00%	95.61%
45	6	0.67%	96.29%
46	1	0.11%	96.40%
47	1	0.11%	96.51%
48	4	0.45%	96.96%
49	3	0.34%	97.30%
50	3	0.34%	97.64%
51	1	0.11%	97.75%
52	0	0.00%	97.75%
53	1	0.11%	97.86%
54	0	0.00%	97.86%
55	0	0.00%	97.86%
56	2	0.22%	98.09%
57	1	0.11%	98.20%
58	1	0.11%	98.31%
59	2	0.22%	98.54%
60	0	0.00%	98.54%
61	1	0.11%	98.65%
62	2	0.22%	98.88%
63	0	0.00%	98.88%
64	1	0.11%	98.99%
65	0	0.00%	98.99%
66	0	0.00%	98.99%
67	0	0.00%	98.99%
68	0	0.00%	98.99%
69	0	0.00%	98.99%
70	2	0.22%	99.21%
71	1	0.11%	99.33%
72	0	0.00%	99.33%
73	0	0.00%	99.33%
74	1	0.11%	99.44%
75	0	0.00%	99.44%
76	0	0.00%	99.44%
77	1	0.11%	99.55%
78	0	0.00%	99.55%
79	1	0.11%	99.66%
80	0	0.00%	99.66%
81	0	0.00%	99.66%
82	0	0.00%	99.66%
83	0	0.00%	99.66%
84	0	0.00%	99.66%
85	2	0.22%	99.89%
86	0	0.00%	99.89%
87	1	0.11%	100.00%

99 Days Window :

94 days	868	Percentage	Cumulative Freq
0	91	10.48%	10.48%
1	192	22.12%	32.60%
2	98	11.29%	43.89%
3	74	8.53%	52.42%
4	53	6.11%	58.53%
5	33	3.80%	62.33%
6	19	2.19%	64.52%
7	35	4.03%	68.55%
8	17	1.96%	70.51%
9	19	2.19%	72.70%
10	17	1.96%	74.65%
11	14	1.61%	76.27%
12	13	1.50%	77.76%
13	6	0.69%	78.46%
14	8	0.92%	79.38%
15	17	1.96%	81.34%
16	5	0.58%	81.91%
17	11	1.27%	83.18%
18	9	1.04%	84.22%
19	11	1.27%	85.48%
20	4	0.46%	85.94%
21	6	0.69%	86.64%
22	10	1.15%	87.79%
23	5	0.58%	88.36%
24	7	0.81%	89.17%
25	0	0.00%	89.17%
26	2	0.23%	89.40%
27	7	0.81%	90.21%
28	0	0.00%	90.21%
29	6	0.69%	90.90%
30	5	0.58%	91.47%
31	6	0.69%	92.17%
32	1	0.12%	92.28%
33	6	0.69%	92.97%
34	1	0.12%	93.09%
35	1	0.12%	93.20%
36	5	0.58%	93.78%
37	3	0.35%	94.12%
38	2	0.23%	94.35%
39	3	0.35%	94.70%
40	4	0.46%	95.16%
41	1	0.12%	95.28%
42	0	0.00%	95.28%
43	4	0.46%	95.74%
44	0	0.00%	95.74%
45	3	0.35%	96.08%
46	0	0.00%	96.08%
47	2	0.23%	96.31%
48	3	0.35%	96.66%
49	2	0.23%	96.89%
50	3	0.35%	97.24%
51	1	0.12%	97.35%
52	0	0.00%	97.35%
53	2	0.23%	97.58%
54	0	0.00%	97.58%
55	0	0.00%	97.58%
56	2	0.23%	97.81%
57	1	0.12%	97.93%
58	1	0.12%	98.04%
59	2	0.23%	98.27%
60	0	0.00%	98.27%
61	1	0.12%	98.39%
62	2	0.23%	98.62%
63	0	0.00%	98.62%
64	1	0.12%	98.73%
65	1	0.12%	98.85%
66	0	0.00%	98.85%
67	0	0.00%	98.85%
68	0	0.00%	98.85%
69	0	0.00%	98.85%
70	3	0.35%	99.19%
71	1	0.12%	99.31%
72	0	0.00%	99.31%
73	0	0.00%	99.31%
74	0	0.00%	99.31%
75	0	0.00%	99.31%
76	0	0.00%	99.31%
77	1	0.12%	99.42%
78	0	0.00%	99.42%
79	1	0.12%	99.54%
80	0	0.00%	99.54%
81	0	0.00%	99.54%
82	0	0.00%	99.54%
83	0	0.00%	99.54%
84	0	0.00%	99.54%
85	1	0.12%	99.65%
86	1	0.12%	99.77%
87	1	0.12%	99.88%
88	0	0.00%	99.88%
89	0	0.00%	99.88%
90	0	0.00%	99.88%
91	0	0.00%	99.88%
92	0	0.00%	99.88%
93	0	0.00%	99.88%
94	1	0.12%	100.00%